数学书上有鬼照片 并非鬼,是数学课本上的怪异现象
1、数学书上有鬼是谣言。这种说法多源于一些配图的视觉误解等等,学生书本都会经过多次检查不会出现大问题漏洞,况且现实生活中并没有鬼,也不用相信书上有鬼的说法。
2、之所以说数学书上有鬼是因为二年级上册数学书本的封面上,有三个小朋友,书本的最右边看起来是一个舞龙的,用放大镜看有一只手露了出来,并且这只手只有四根手指,对此有人反驳,不用放大镜看的话就是一个花蕊,而那些说是手指的人纯属有意的制造恐慌,不必理会。
3、数学书上有鬼图片这种说法都是一些成年人的过度解读,并不是真的。相关的谣言不外乎就是什么数学书上披头散发不像护士的护士拿着体温表给病人说显示98.6度,没发烧,很像是鬼,对此有人解释98.6度是华氏度等于37摄氏度所以没有发烧,跟鬼无关。所以大家不要以讹传讹。数学书上有鬼照片,并非鬼,是数学课本上的怪异现象。
基于这件事情的严重性,基于一个成年人应该为社会承担的责任,我决定自己发表一篇文章。
本篇主要搜集了那些有代表性的“妖图”。

作为一个心理健康的成年人,我看到这张图,都不愿意盯着看超过一秒钟。太难受了。好像小孩子被虐待之后,屈服于施暴者的淫威下,被逼着摆出开心的样子拍照。天哪,被深深的变态的感觉恶心到了。7、8岁的孩子是什么感觉呢!
这是什么玩意,教科书里居然有鬼!
不,书里没鬼,书外创作、审批,每层的关键位置一定都是鬼!
我不敢相信!这是现在的文明社会里国家教育体系的课本里会出现的图,而且还是面对儿童的“必读书”。
全书据说没有中国国旗,这其实没什么。但是在没有祖国国旗的背景下,这个印着美国国旗的衣服实在是讽刺、刺眼。
这是鲶鱼精吧!
我看到这些图无意识的就想挑挑眉,睁睁眼,感觉眼皮好沉重,整个人都不好了。
无意冒犯,但他会帮助国人直观认识到咱们关键部位的蛆虫是多么的下三滥。
这是唐氏综合征患者。(衷心希望这个病被彻底灭绝)
清华美院,呵呵。
拿着国家给的高额补助,学出来就是这么回报国家的嘛!!!
我就不信这次文章连接还会丢失!
气愤!
呼吁成年人,站出来给社会正确的反馈。这是我们的责任也是义务。
保护祖国,从花朵开始!
小学语文教材书上有“鬼”?家长发视频质疑,却遭到网友疯狂嘲讽=====给孩子们讲的“鬼”数学课=====《数学之书》的翻译问题(上) “教材书插图”一事,近几日闹得沸沸扬扬,某一教材插图人物目光呆滞,毫无生气可言。除了教材书有问题,部分教辅也被曝光,某些书籍的“民歌过于露骨”“词语用法不当”等等。====
接上篇与几个孩子围坐一起,讲鬼故事
听我讲了“莫言的小红孩儿鬼”,有个小姑娘抢过话头说:
“哦,我想起一个,也有过河,叫宋定伯卖鬼。”
《宋定伯捉鬼》出自晋人干宝的《搜神记》,是唐以前的故事,有趣味。讲南阳人宋定伯胆大精明,不但不怕鬼,还把鬼骗到市场变作绵羊给卖了。
小家伙讲时,笑得厉害,说“鬼真是个大笨蛋”。
讲完我问:如果我们是那只鬼,怎么看宋定伯呢?

你们慢慢想,不用现在答,有机会再告诉我。为了方便你们换位思考,我今天当回数学老师,给你们讲讲人和鬼的数学关系。
咱们中国文化传统里的鬼是什么呢?
有人认为,鬼就是人死后徘徊在人世间的魂。
那魂是什么呢?
魂是人区别于其它动物而独有的灵性,是在动物性上进化发展出来的高级部分。魂很轻,可以飞,甚至瞬间转移。我们语文里就有个成语叫魂飞魄散。
那魄是什么呢?
有人说魄就是人身上的动物性,要吃、要睡、要羞羞。
魂飞魄散后,就剩个不会动、也没有思想的死身体。
我先给你们一个公式:人=魂+魄+身体。
不好理解吧,不急,听我慢慢讲。
有个清朝人的笔记中记着这么一则故事:
说有个年轻的后生,随父亲去四川上任地方官。蜀道艰难,后生不小心落马坠下山崖。与此同时,百里之外的一个刚刚去世的中年男人,突然从病床上坐起,大叫一声:“摔死我啦!”
更奇怪的是,这中年男人醒来后,不识老母,不认妻儿。接过旁人递来的镜子,瞅着镜中陌生的麻子脸,不住地说:
“这个人不是我,这个人不是我。我还没有结婚,我姓王,正跟着我的父亲去四川......”
怎么回事呢?
原来是这个年轻人的魂在摔下山崖时飞了,落在了这个刚死的麻脸中年男人的体魄上。
在我们中国的鬼故事里,人是可以组装的。魂飞了,这个人死了,但可能活到另一个人身上去。当然魄散了,人也会死。那问两个数学题:魂+身体=?魄+身体=?
我刚才说了,鬼就是魂。魂是有灵性的,所以我们称之为灵魂。灵魂是看不见的。我们只能在文字、话语、事迹中,评判出一个人灵魂的高尚或丑陋。

那书籍或影视作品里那些肉眼看得到的鬼是什么呢?是“魂+身体”。
那“魄+身体”是什么呢?我刚才讲过,魄是动物性的,所以加起来是僵尸。僵尸就是个奇怪的动物。清朝人袁枚在《子不语》中写过一个僵尸,跑来跑去找小孩子吃。
 中外僵尸交流
中外僵尸交流
还有,“魂+魄”是什么呢?按我的公式,“魂+魄”不能长久存在,为什么呢?因为魄是动物性的,它要吃要喝的呀,几天不吃饭,魄就散了,又只剩下魂了。
好,最后,我再把所有公式列一遍:
人=魂+魄+身体
鬼=魂(无形)=魂+身体(有形)
僵尸=魄+身体(是个奇怪的动物)
所以你们看鬼,要当它是个不完整的人,是人身上很有意思的一部分。僵尸就是个动物,有的温良有的暴躁,只是长着人身体坏掉了的样子。
好啦,今天这个“鬼”数学课就到这里了。我讲明白了吗?
2019年11月12日早,大观园
====
作者 | 究究谢
来源 | 孔夫子旧书网动态
《数学之书》通过数学史上250个里程碑式的发现,带读者发现数学之美。这是“一部图文并茂的编年体数学百科,一卷博古通今的数学历史,故事性趣味性知识性完美融合!一本书让您领略科学之王——数学的迷人魅力!”该书荣获科技部2016年全国优秀科普作品奖!
科普鬼才作者克利福德·皮寇弗是一位多产作家,涉猎主题从科学、数学到宗教、艺术及历史,出版超过四十本书,并被翻译成数十种语言,畅销全球。皮寇弗在耶鲁大学取得分子生物理化博士学位,在美国拥有四十多项专利,并担任数本科学期刊的编辑委员。他的研究屡屡见于CNN、《连线》杂志、《纽约时报》等诸多重要媒体。


长期以来,我一直以为港台译本的质量不错,毕竟港台学生的英语功底往往比大陆学生要扎实些。因此,我看到重庆出版社2015年引进台湾人陈以礼翻译、台湾师大数学系退休教授洪万生审定的这本《数学之书》,竟然也是“一颗被猪拱了的好白菜”,真很有些吃惊。
这里还是按老规矩,以英文原版、我的译文、台湾译文三对照的形式给出序言部分。可以看到,里面不仅有许多低级错误,还有不少台湾与大陆术语的不同用法,我们出版社引进港台版书时也不能太轻率盲信了。我也想对各家出版社说一句:被猪拱过的白菜只能拿去喂猪,不好再给人吃了!
=============================
Introduction The Beauty and Utility of Mathematics
【我译】引言 数学之美与用
简介数学之美与效用
“Anintelligent observer seeing mathematicians at work might conclude that they aredevotees of exotic sects, pursuers of esoteric keys to the universe.”
—Philip Davisand Reuben Hersh, The Mathematical Experience
【我译】聪慧的观察者在看着数学家开展工作时,大概会认为他们是虔诚的密宗信徒,是追寻开启宇宙奥秘密钥的人。
——菲利浦·戴维斯(Philip Davis)与鲁本·赫什(Reuben Hersh),《数学体验》(The Mathematical Experience)一书作者
聪慧的观察者看过数学家所从事的工作后,大概会认为他们是一群狂热流派奉献者,宇宙的神秘钥匙的追寻者。
——戴维斯(PhilipDavis)与赫什(Reuben Hersh),
《数学经验谈》(TheMathematical Experience)一书作者
Mathematics has permeated every field of scientificendeavor and plays an invaluable role in biology, physics, chemistry,economics, sociology, and engineering. Mathematics can be used to help explainthe colors of a sunset or the architecture of our brains. Mathematics helps usbuild supersonic aircraft and roller coasters, simulate the flow of Earth’snatural resources, explore subatomic quantum realities, and image farawaygalaxies. Mathematics has changed the way we look at the cosmos.
【我译】数学已经渗透到了科学事业的各个领域,并且在生物学、物理、化学、经济学、社会学和工程等学科中发挥着不可估量的作用。我们可以用数学来解释夕阳绚丽的色彩,也可以用它来说明人类大脑的结构。数学帮助我们制造超音速飞机和云霄飞车,模拟地球自然资源的流转,探索亚原子级的量子世界,并对遥远的星系进行成像。数学改变了我们看待宇宙的方式。
数学已经渗入每一个需要费尽心思去理解的科学领域,并且在生物学、物理、化学、经济、社会学和工程等方面取得无法替代的角色。我们可以用数学说明夕阳色彩分布的情况,也可以用来说明人类的大脑结构。数学帮助我们打造超音速飞机和云霄飞车,模拟地球天然资源流转的方式,进入次原子粒子的量子世界探索,甚至让我们得以想象遥远的银河系。可以说,数学改变了我们看待宇宙的方式。
In this book, I hope to give readers ataste for mathematics using few formulas, while stretching and exercising theimagination. However, the topics in this book are not mere curiosities withlittle value to the average reader. In fact, reports from the U.S. Departmentof Education suggest that successfully completing a mathematics class in highschool results in better performance at college whatever major the student choosesto pursue.
【我译】在本书中,我希望用少量数学公式让读者通过施展和发挥想象力,去品尝一下数学的滋味。但是,对普通读者而言,本书所探讨的主题并非仅能满足好奇心却没什么价值的东西。事实上,来自美国教育部的报告表明,在高中阶段顺利学完了数学课程的学生,上大学后不论选读哪个专业,都能取得更好的成绩。
在本书中,我希望运用少量数学公式提供一点数学品位,而鼓励读者发挥想象力。对大多数读者而言,这本书所谈论的应该不只是能满足好奇心却缺乏实用价值的单元,根据美国教育部实际调查的结果显示,能够顺利完成高中数学课程的学生升上大学后不论选读哪一个专业,都能展现出比较优秀的学习能力。
The usefulness of mathematics allows us tobuild spaceships and investigate the geometry of our universe. Numbers may beour first means of communication with intelligent alien races. Some physicistshave even speculated that an understanding of higher dimensions and oftopology—the study of shapes and their interrelationships—may someday allow usto escape our universe, when it ends in either great heat or cold, and then wecould call all of space-time our home.
【我译】数学的实用性让我们得以建造宇宙飞船,并探索所处宇宙的几何结构。数字也可能是我们与智能外星生物进行沟通的首要途径。有些物理学家认为,对高维空间和拓扑学(探讨形状及其相互关系的一门学问)的理解,或许有朝一日能让我们逃离将处于极热或极冷末日的这个宇宙,届时我们可将整个时空当成自己的家园。
数学的实用性让我们可以建造宇宙飞船,探索所处宇宙的几何结构。数字也可能是我们与有智能的外星生物间所采用的第一种沟通手段。有些物理学家认为掌握更高空间维度和拓扑学(topology,探索形状与彼此间相互关系的一门学问),或许有一天当现在这个宇宙处于在极热或极冷的末日之际,我们就能逃出,在不同的时空环境下安身立命。
Simultaneous discovery has often occurredin the history of mathematics. As I mention in my book The Mbius Strip, in1858 the German mathematician August Mbius (1790–1868) simultaneously andindependently discovered the Mbius strip (a wonderful twisted object with justone side) along with a contemporary scholar, the German mathematician JohannBenedict Listing (1808–1882). This simultaneous discovery of the Mbius band byMbius and Listing, just like that of calculus by English polymath Isaac Newton(1643–1727) and German mathematician Gottfried Wilhelm Leibniz (1646–1716),makes me wonder why so many discoveries in science were made at the same timeby people working independently. For another example, British naturalists CharlesDarwin (1809–1882) and Alfred Wallace (1823–1913) both developed the theory ofevolution independently and simultaneously. Similarly, Hungarian mathematicianJános Bolyai (1802–1860) and Russian mathematician Nikolai Lobachevsky(1793–1856) seemed to have developed hyperbolic geometry independently, and atthe same time.
【我译】数学史上经常出现不同人同时作出重大发现的事例。我在拙作《莫比乌斯带》中提到过,德国数学家莫比乌斯(August Mbius,1790–1868)和当时的另一位学者——德国数学家利斯廷(Johann Benedict Listing,1808–1882),同时在1858年各自独立地发现了莫比乌斯带(一个只有单面的神奇扭曲体)。莫比乌斯和利斯廷同时作出的这项重大发现,就像英国博学多闻的牛顿(1643–1727)与德国数学家莱布尼兹(1646–1716)各自同时发现的微积分一样,让我不禁好奇为何会有这么多科学发现,是由独自工作的人在相同的时间作出的呢?再举一个例子,英国博物学家查尔斯·达尔文(1809–1882)和阿尔弗雷德·华莱士(1823–1913),两人同时独自提出了进化论。与此类似,匈牙利数学家鲍耶(JánosBolyai,1802–1860)和俄罗斯数学家罗巴切夫斯基(Nikolai Lobachevsky,1793–1856),似乎也是同时独自提出了双曲几何的思想。
数学史上不乏许多人同步有重大发现的例子,就以这本书中的莫比乌斯带为例。德国数学家莫比乌斯(August Mbius)和当时另一位德国数学家利斯廷(Johann Benedict Listing)同时在1858年各自发现莫比乌斯带(一个只有单面,神奇的扭曲物体)。这种同步发现的现象就跟英国博学多闻的牛顿(Isaac Newton)与德国数学家莱布尼兹(Gottfried Wilhelm Leibniz)各自同时发现微积分的例子相似。这些例子让我不禁怀疑科学领域为何经常有不同人,在相同时间,独立发现同一件事情的情况?其他例子还包括英国博物学家达尔文(Charles Darwin)和华莱士(Alfred Wallace)都在相同时间各自提出演化论的观点,匈牙利数学家鲍耶(János Bolyai)和俄罗斯数学家罗巴切夫斯基(Nikolai Lobachevsky)似乎也是在同一时间各自提出双曲几何的想法。
Most likely, such simultaneous discoverieshave occurred because the time was ripe for such discoveries, given humanity’saccumulated knowledge at the time the discoveries were made. Sometimes, twoscientists are stimulated by reading the same preliminary research of one oftheir contemporaries. On the other hand, mystics have suggested that a deepermeaning exists to such coincidences. Austrian biologist Paul Kammerer(1880–1926) wrote, “We thus arrive at the image of a world-mosaic or cosmickaleidoscope, which, in spite of constant shuffling and rearrangements, alsotakes care of bringing like and like together.” He compared events in our worldto the tops of ocean waves that seem isolated and unrelated. According to hiscontroversial theory, we notice the tops of the waves, but beneath the surfacesome kind of synchronistic mechanism may exist that mysteriously connectsevents in our world and causes them to cluster.
【我译】最有可能的解释是,之所以会出现这些同时作出的发现,是因为在作出这些发现时,人类已累积了足够的知识,这些发现已到了瓜熟蒂落的时候。有时,是两位科学家读到同时代另一个人的同一篇先导性研究报告,受到了启发。另一方面,神秘主义者提出过这种观点,认为此类巧合中蕴含着更深层的意义。奥地利生物学家卡摩尔(Paul Kammerer,1880–1926)曾在文章中表示:“在镶嵌图案似的世界或万花筒似的宇宙中,我们看到了这样的景象——尽管经历过不断的打散和重组,却总是能物以类聚。”他把现实世界中的事件比作海洋波涛的峰顶,貌似各自孤立、毫无瓜葛。按照他这种充满争议的理论,我们看到的只是波峰,而在其表面之下可能存在着某种同步机制,把世上的一些事件联系在一起,让它们扎堆出现。
最有可能解释同步重大发现的理由,是因为人类在那些时间点对于即将诞生的发现,已经累积足够的知识,这些想法自然也就瓜熟蒂落地被提出来;可能两位科学家都受到当代其他研究人员同一篇先导研究论文的影响。另一种带有神秘色彩的解释,会从较深层的观点说明这种巧合。奥地利生物学家卡梅纳(Paul Kammerer)曾表示:“或许我们可以说,尽管打散、重组的过程在现实世界繁华的表面下与宇宙无垠的千变万化中不断重复发生,但是物以类聚的现象也会同时在这些过程中产生”;卡梅纳把现实世界的重大*事件比喻成海洋波涛的顶端,彼此间看起来各自孤立,毫无瓜葛,不过根据他充满争议性的理论,我们其实只看到上层的波浪,却没注意到海面下可能存在某种同步机制,诡谲地把世上各种重大*事件串在一起,才显现出这种一波又一波的风潮。
Georges Ifrah in The Universal History ofNumbers discusses simultaneity when writing about Mayan mathematics:
We therefore see yet again how people whohave been widely separated in time or space have…been led to very similar ifnot identical results…. In some cases, the explanation for this may be found incontacts and influences between different groups of people….The trueexplanation lies in what we have previously referred to as the profound unityof culture: the intelligence of Homo sapiens is universal and its potential isremarkably uniform in all parts of the world.
【我译】易法拉(Georges Ifrah)在《数字全史》(The Universal History of Numbers)一书中写到玛雅数学时,也讨论了这种同时性问题:
我们因而又再一次看到,在时间或空间上相距甚远的人是如何……得出非常类似甚至是完全相同的结论……有时,也许可以在不同人群间的接触和影响中,找到对这一点的解释……真正的解释在于我们前面所谓的深层文化融合:智人的智慧具有共通性,其潜力在世界各地惊人地一致。
易法拉(GeorgesIfrah)在《数目溯源》(TheUniversal History of Numbers)一书中谈论玛雅数学时,顺便论及了这种同步情况:
我们因此又再一次地见证,散居在广大时空环境下互不认识的人……也会有非常类似甚至是一模一样的想法。……有些例子的解释;是因为他们接触了另一群不一样的人并受到对方的影响……真正的有效解释是因为前面提过的深层文化融合:智人(Homo sapiens)这种生物的智力具有共通性,把世界各个角落统整串连的潜力非常可观。
Ancient people, like the Greeks, had a deepfascination with numbers. Could it be that in difficult times numbers were theonly constant thing in an ever-shifting world? To the Pythagoreans, an ancientGreek sect, numbers were tangible, immutable, comfortable, eternal—morereliable than friends, less threatening than Apollo and Zeus.
【我译】古人(比如古希腊人)对数字非常痴迷。是不是因为在艰难岁月中,在一个变动不居的世界上,唯有数字才是恒常不变的东西?对于毕达哥拉斯学派(古希腊的一个秘密学派),数字是触手可及的、不变的、令人心安的、永恒的——比朋友更可靠,又不像阿波罗或宙斯那么令人敬畏。
古代的希腊人受到数字深深的吸引。在这个不停变动的世界,会不会只有数字才是唯一恒常不变的?对于源自一门古希腊学派、毕达哥拉斯理念的追随者而言,数字是具体不变和缓永恒的——比所有朋友更值得信赖,却不像阿波罗或宙斯般让人无法亲近。
Many entries in this book deal with wholenumbers, or integers. The brilliant mathematician Paul Erds (1913–1996) wasfascinated by number theory—the study of integers—and he had no trouble posingproblems, using integers, that were often simple to state but notoriouslydifficult to solve. Erds believed that if one can state a problem inmathematics that is unsolved for more than a century, then it is a problem innumber theory.
【我译】本书中许多条目讨论的都是整数。杰出的数学家埃尔德什(Paul Erds,1913–1996) 醉心于数论——研究整数的学问——他可以毫不费力地用整数提出一些表述起来很简单、解答起来却难得出奇的问题。埃尔德什认为,一个数学问题如果被提出来之后,过了一个世纪仍然没人解答得了的话,那一定是个数论问题。
本书中有很多条目都跟整数有关,聪颖的数学家艾狄胥(Paul Erdos)醉心于数论——有关于整数课题的研究,他经常能轻易使用整数提出问题,尽管问题的陈述很简单,但是每一题却都是出了名的难解。艾狄胥认为如果有任何数学问题提出后经过一个世纪依然无解的话,那一定是个与数论有关的问题。
Many aspects of the universe can beexpressed by whole numbers. Numerical patterns describe the arrangement offlorets in a daisy, the reproduction of rabbits, the orbit of the planets, theharmonies of music, and the relationships between elements in the periodictable. Leopold Kronecker (1823–1891), a German algebraist and number theorist,once said, “The integers came from God and all else was man-made.” Hisimplication was that the primary source of all mathematics is the integers.
【我译】宇宙的很多方面都可以用整数来表达。数值模式可以用来描述雏菊花瓣的排列、兔子的繁衍、行星的轨道、音乐的和弦以及周期表中元素间的关系。德国代数学家、数论大师克罗内克(Leopold Kronecker,1823–1891)曾经说过:“整数来自上帝,其他一切皆是人为。”这句话意味着整数是一切数学的主要根源。
有很多宇宙万物可以用整数来表达,譬如用整数描述菊花花瓣构成的方式、兔子的繁衍、行星的轨道、音乐的和弦以及周期表元素间的关系。德国代数学家暨数论大师克罗内克(Leopold Kronecker)曾经说过:“只有整数来自于上帝,其他都是人造的。”这句话也暗示整数是一切数学的最主要根源。
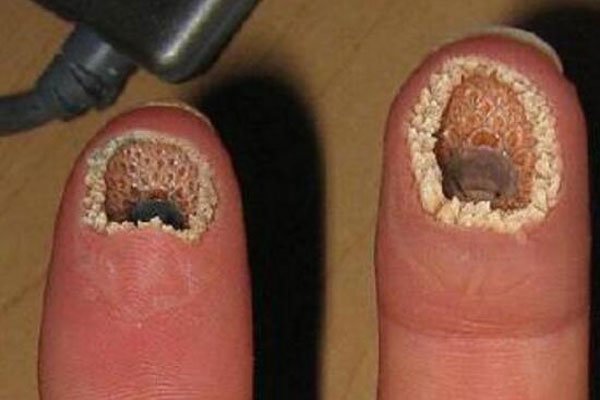 空空指是什么引起的 网上流出的ps图片很吓人
空空指是什么引起的 网上流出的ps图片很吓人[娱乐综合]编辑:洋洋2023-04-21
几年前,网上特别火的两组照片就是空手指和蓬蓬乳了,让人看后不寒而栗,这让人不得不想到,空空指是什么引起的?网上流出的ps图片很吓人,这到底是PS的还是真实存在的疾病呢?如果是真实存在的,患…… 查看全文>>
 红婶真实存在吗 不是真的(鬼女魔咒里虚构的角色)
红婶真实存在吗 不是真的(鬼女魔咒里虚构的角色)[娱乐综合]编辑:夏天2023-04-21
红婶真实存在吗?不是真的(鬼女魔咒里虚构的角色)?关于红婶的信息也不是很多,那么就来简单的看一看网络中对于红婶最恐怖的照片介绍是什么吧!真人挺可爱怎么会那么吓人?还是不了解她为什么会那么…… 查看全文>>
 红姨是什么意思 超恐怖女鬼千万不能搜(样子吓人)
红姨是什么意思 超恐怖女鬼千万不能搜(样子吓人)[娱乐综合]编辑:夏天2023-04-21
红姨全称是红衣女,是一个出现在日本恐怖片《鬼女魔咒》里面的“鬼”角色,扮演者是小林裕子。单独拿出来说是指一些比较恐怖的人和事。红姨是一个出现在日本恐怖片《鬼女魔咒之红衣女篇》里面的“鬼…… 查看全文>>
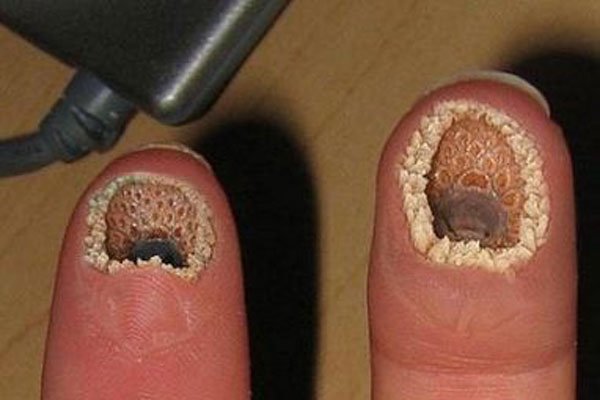 莲蓬乳,空空指,微笑狗,牙膏脸是什么意思 建议密集恐惧症的人远离
莲蓬乳,空空指,微笑狗,牙膏脸是什么意思 建议密集恐惧症的人远离[娱乐综合]编辑:橘子2023-04-21
莲蓬乳,空空指,微笑狗,牙膏脸是什么意思?建议密集恐惧症的人远离,最近网上突然流传搜索“莲蓬乳、空手指、牙膏脸、微笑狗”等照片和视频,可以说是好奇心作祟,奉劝心理承受能力不强和有…… 查看全文>>
 小石潭记其实是个鬼故事 背后的恐怖真相(到底多可怕)
小石潭记其实是个鬼故事 背后的恐怖真相(到底多可怕)[娱乐综合]编辑:橘子2023-04-21
相信大家一定在上学的时候学过不少古文吧,书上的每一篇古文都可以说是非常优秀的,是我国古代文化的艺术瑰宝。《小石潭记》相信大家一定并不陌生,这是柳宗元所写的一篇游记,文笔非常优美,但其实…… 查看全文>>

- 三年级上册语文书有鬼 没鬼,最恐怖的就是背诵全文
- 三年级上册语文书有鬼?没有鬼,假的,三年级上册语文...
- 查看详情>>

- 一道数学题难倒13亿人 坑人套路数学题带答案
- 数学题向来是让很多人头疼的难题,尤其是有些问题如果...
- 查看详情>>

- 夜明珠到底是什么东西为什么会发光 最大的夜明珠是哪里发现的
- 世界上最大的夜明珠重量为8.53吨,它的直径有1.72米。...
- 查看详情>>

- 爱因斯坦手稿高清图片 他的手稿以多少钱成交了
- 近期以色列希伯来大学首次公布了爱因斯坦的110份手稿...
- 查看详情>>

- 堕胎的果报与化解方法真相 堕胎的孩子去了哪里
- 每一个婴儿健康的来到这个世界上,就是给父母最好的礼...
- 查看详情>>

- 血腥的hello kitty藏尸案件始末 作案过程细节是怎么回事
- 在香港出现的杀人案特别的多,而且都特别的丧心病狂。...
- 查看详情>>

- 赣江的源头和终点在哪 赣江源头到底在哪
- 赣江的源头和终点在哪,赣江源头到底在哪?赣江的源头...
- 查看详情>>